Байесовская линейная регрессия: что это такое, функции и приложения в реальной жизни в 2022 году

Что такое линейная регрессия?

Линейная регрессия пытается показать связь между двумя факторами, подбирая прямое условие к замеченной информации. Одна переменная рассматривается как иллюстративная переменная, а другая рассматривается как необходимая переменная. Например, модельер должен связать множество людей со своими статуями, используя модель прямого рецидива.

Теперь следующий шаг — узнать, что такое линейное уравнение Байеса и как его можно рассчитать, чтобы получить желаемый результат.

Теперь, что такое байесовское линейное уравнение?

Итак, когда мы говорим о байесовских методах регрессии, мы знаем, что это очень мощный метод, потому что они предоставляют нам полное распределение по параметрам регрессии. Для расчета неадекватных данных или неравномерно распределенных данных байесовская линейная регрессия предоставляет естественный механизм.

Вы можете разместить априорные коэффициенты так, чтобы при отсутствии данных априор мог занять место данных. Статистический анализ проводится в условиях байесовского интерфейса в байесовской линейной регрессии в статистике.

Мы используем распределение вероятностей вместо точечных оценок для разработки линейной регрессии.

Результат достигается за счет распределения вероятностей, а не за счет обычных методов регрессии. Цель байесовской линейной регрессии — найти апостериорную модель вместо параметров модели.

Предполагается, что параметры модели происходят из распределения.

Апостериорное выражение

Апостериорная = (вероятность * априорная) / нормализация

Приведенное выше уравнение похоже на теорему Байеса, которая

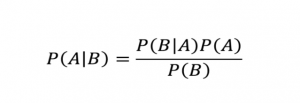
Источник

Реальное применение байесовской линейной регрессии

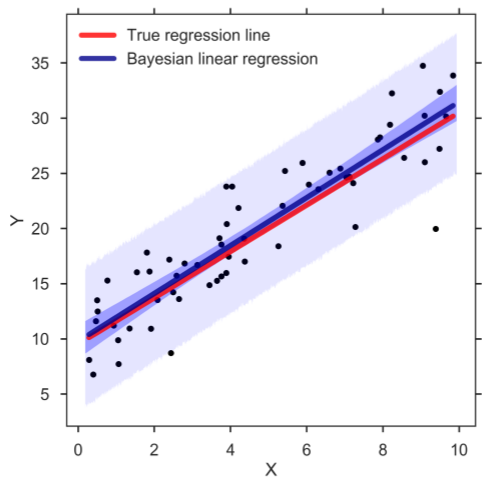
Согласно следующим графикам, линейная регрессия и байесовская регрессия могут давать одинаковые прогнозы.

Источник

Источник

На последнем графике мы можем предположить, что если прогностическое распределение находится внутри толстого цвета, то плотность данных высокая, а если оно находится в дефицитной области, плотность можно считать низкой.

Давайте поговорим о преимуществах байесовской регрессии:

• С помощью байесовской обработки мы можем получить все разнообразие выводных решений вместо точечной оценки.
• Он эффективно работает с небольшим размером набора данных.
• Это очень подходит для онлайн-формы обучения, тогда как в форме пакетного обучения у нас есть весь набор данных.
• Это очень мощный и проверенный подход.

Теперь поговорим о недостатках байесовской линейной регрессии.

• Это не работает эффективно, если набор данных содержит огромное количество данных.
• Гипотеза модели может занять много времени.

Читайте: Идеи и темы для линейных проектов

Заключение

Итак, мы видим, какой мощный метод байесовской линейной регрессии. С помощью байесовской линейной регрессии можно получить множество преимуществ, и это один из естественных механизмов для расчета недостаточных или плохо распределенных данных.

Байесовская точка зрения — это инстинктивная форма видения мира. Своему частому аналогу байесовский вывод может приукрасить очень удобную замену. Он используется в различных областях, таких как наука о данных, машинное обучение и многие другие. Это помогает в построении различных моделей, с помощью которых мы можем решить множество задач.

Если вы хотите узнать больше о карьере в области машинного обучения и искусственного интеллекта, ознакомьтесь с IIT Madras и расширенной сертификацией upGrad в области машинного обучения и облачных вычислений.