Байесовская статистика и модель: объяснение

Байесовский метод — это подход в статистике, используемый для анализа данных и оценки параметров. Этот подход основан на теореме Байеса.

Байесовская статистика следует уникальному принципу, в котором она помогает определить совместное распределение вероятностей для наблюдаемых и ненаблюдаемых параметров с использованием статистической модели. Знание статистики необходимо для решения аналитических задач в этом сценарии.

С тех пор, как в 1770-х годах Томас Байес представил теорему Байеса, она остается незаменимым инструментом в статистике. Байесовские модели являются классической заменой частотных моделей, поскольку недавние инновации в статистике помогли преодолеть вехи в широком спектре отраслей, включая медицинские исследования, понимание веб-поиска и обработку естественных языков (обработку естественного языка).

Например, известно, что болезнь Альцгеймера представляет прогрессирующий риск с возрастом человека. Однако с помощью теоремы Байеса врачи могут оценить вероятность появления у человека болезни Альцгеймера в будущем. Это также относится к раку и другим возрастным заболеваниям, которым человек становится уязвимым в более поздние годы своей жизни.

Частая статистика против байесовской статистики

Частая статистика против байесовской статистики постоянно была темой споров и ночных кошмаров для новичков, которым трудно сделать выбор между ними. В начале 20 века байесовская статистика столкнулась с проблемами недоверия и принятия. Однако со временем люди осознали применимость байесовских моделей и точные решения, которые они дают.

Вот взгляните на частую статистику и сложности, связанные с ними:

Частая статистика

Это широко используемая методология вывода в мире статистики. Он анализирует, произошло ли событие (упомянутое как гипотеза). Он также оценивает вероятность события, происходящего в течение эксперимента. Эксперимент повторяется до тех пор, пока не будет достигнут желаемый результат.

Их выборки распределения имеют реальный размер, и теоретически эксперимент повторяется бесконечное количество раз. Вот пример, показывающий, как частую статистику можно использовать для изучения подбрасывания монеты.

• Вероятность выпадения орла при однократном подбрасывании монеты равна 0,5 (1/2).
• Количество голов обозначает фактическое количество полученных лидов.
• Разница между фактическим количеством орлов и ожидаемым количеством орлов будет увеличиваться по мере увеличения количества подбрасываний.

Так что здесь результат зависит от того, сколько раз повторяется эксперимент. Это главный недостаток частой статистики.

Другие недостатки, связанные с его дизайном и методами интерпретации, стали очевидны в 20-м веке, когда применение частой статистики к числовым моделям было на пике.

Ограничения часто используемой статистики

Три основных недостатка частой статистики перечислены ниже:

1. Переменные значения p

Значения p, измеренные для выборки фиксированного размера в эксперименте с определенной конечной точкой, изменяются при любом изменении конечной точки и размера выборки. Это приводит к двум значениям p для одних данных, что неверно.

2. Непоследовательные доверительные интервалы

ДИ (доверительный интервал) зависит исключительно от размера выборки. Это делает тормозной потенциал несущественным.

3. Расчетные значения ДИ

Доверительные интервалы не являются распределением вероятностей, и их значения для параметра являются только оценкой, а не фактическими значениями.

Вышеупомянутые три причины породили байесовский подход, который применяет вероятности к статистическим задачам.

Рождение байесовской статистики

Преподобный Томас Байес впервые предложил байесовский подход к статистике в своем эссе, написанном в 1763 году. Этот подход был опубликован Ричардом Прайсом как стратегия обратной вероятности для прогнозирования будущих событий на основе прошлого.

Подход основан на теореме Байеса, которая поясняется ниже:

Теорема Байеса

Аксиома вероятности Реньи исследует условные вероятности, где возможности возникновения события A и события B являются зависимыми или условными. Основная условная вероятность может быть записана как:

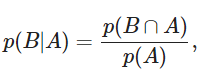
Вероятность наступления события В зависит от события А.

Приведенное выше уравнение является основой правила Байеса, математического выражения теоремы Байеса, которая гласит:

Здесь ∩ обозначает пересечение.

Правило Байеса можно записать так:

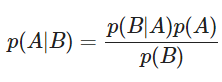
Правило Байеса является основой байесовской статистики, когда доступная информация о конкретном параметре в статистической модели сравнивается и обновляется с помощью собранных данных.

Фоновые знания представлены в виде априорного распределения, которое затем сравнивается и изучается с наблюдаемыми или собранными данными как функция правдоподобия, чтобы выяснить апостериорное распределение.

Это апостериорное распределение используется для предсказания будущих событий.

Применение байесовского подхода зависит от следующих параметров:

1. Определение априорной модели и модели данных
2. Делая соответствующие выводы
3. Проверка и оптимизация моделей

Что такое байесовские нейронные сети?

Байесовские нейронные сети (BNN) — это сети, которые вы создаете, когда расширяете стандартные сети с помощью статистической методологии и изменяете апостериорный вывод, чтобы отслеживать переобучение. Поскольку это байесовский подход, существует распределение вероятностей, связанное с параметрами нейронных сетей.

Они используются для решения сложных проблем, где отсутствует свободный доступ к данным. Байесовские нейронные сети помогают контролировать переоснащение в таких областях, как молекулярная биология и медицинская диагностика.

Используя байесовские нейронные сети, можно рассмотреть все распределение ответов на вопрос, а не только одну возможность. Они помогают определить выбор/сравнение моделей и решать проблемы, связанные с регуляризацией.

Байесовская статистика предлагает математические инструменты для рационализации и обновления субъективных знаний о новых данных или научных доказательствах. В отличие от частого статистического подхода, он работает на основе предположения, что вероятности зависят от частоты повторения событий в одних и тех же условиях.

Короче говоря, байесовский метод является расширением допущения и мнения человека. Ключевым аспектом байесовской модели, который делает ее более эффективной, является понимание того, что люди различаются в своих мнениях в зависимости от того, какую информацию они получают.

Однако по мере появления новых доказательств и данных у людей появляется точка соприкосновения, байесовский вывод . Это рациональное обновление является особенностью байесовской статистики, которая делает ее более эффективной при решении аналитических задач.

Здесь вероятность 0 применяется, когда нет надежды на то, что событие произойдет, а вероятность 1 применяется, когда есть уверенность, что событие произойдет. Вероятность от 0 до 1 дает место для других возможных результатов.

Правило Байеса теперь применяется для достижения байесовского вывода, чтобы получить лучший вывод из модели.

Как применить правило Байеса для получения байесовского вывода?

Рассмотрим уравнение:

P(θ|D) = P(D|θ.)P(θ) / P(D)

P(θ) обозначает априорное распределение,

P(θ|D) обозначает апостериорное убеждение,

P(D) представляет свидетельство,

P(D|θ) указывает вероятность.

Основная цель байесовского вывода состоит в том, чтобы предложить рациональный и математически точный метод смешивания убеждений с доказательствами для получения обновленных апостериорных убеждений. Апостериорные убеждения можно использовать в качестве априорных убеждений, когда генерируются новые данные. Таким образом, байесовский вывод помогает постоянно обновлять убеждения с помощью правила Байеса.

Рассматривая тот же пример с подбрасыванием монеты, байесовская модель обновляет процедуру с предыдущих до апостериорных убеждений с новыми подбрасываниями монеты. Байесовский метод дает следующие вероятности.

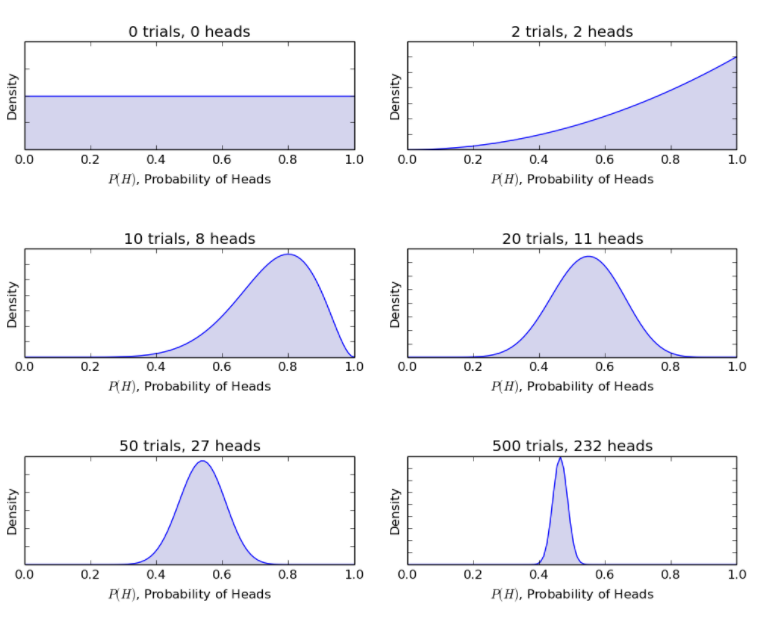
Источник

Таким образом, байесовская модель позволяет свести неопределенный сценарий с ограниченной информацией к более определенному сценарию со значительным объемом данных.

Заметные различия между байесовской моделью и частотной моделью

Частая статистика

Байесовская статистика

Цель считается точечной оценкой, а КИ

Цель рассматривается как апостериорное распределение

Процедура начинается с наблюдения

Процесс начинается с предварительного распределения

Всякий раз, когда делаются новые наблюдения, частотный подход повторно вычисляет существующую модель.

Всякий раз, когда делаются новые наблюдения, апостериорное распределение (идеология/гипотеза) обновляется.

Примеры: оценка среднего, t-критерий и дисперсионный анализ.

Примеры: оценка апостериорного распределения среднего и перекрытия интервалов высокой плотности.

Преимущества байесовской статистики

• Он обеспечивает органичные и простые средства для объединения заранее подготовленной информации с прочной структурой и научными данными. Прошлую информацию о параметре можно использовать для формирования априорного распределения для будущих исследований. Выводы придерживаются теоремы Байеса.
• Выводы из байесовской модели являются логическими и математически точными, а не грубыми предположениями. Точность остается постоянной независимо от размера выборки.
• Байесовская статистика следует принципу правдоподобия. Когда две разные выборки имеют общую функцию правдоподобия для убеждения θ, все выводы об этом убеждении должны быть схожими. Классические статистические методы не следуют принципу правдоподобия.
• Решения байесовского анализа легко интерпретируются.
• Он предлагает удобную платформу для различных моделей, таких как иерархические модели и проблемы с неполными данными. Расчеты всех параметрических моделей можно виртуально отслеживать с помощью других численных методов.

Успешное применение байесовских моделей в истории

Байесовские методы успешно применялись во время Второй мировой войны. Некоторые из них перечислены ниже:

• Российский статистик Андрей Колмогоров успешно использовал байесовские методы для повышения эффективности российской артиллерии.
• Байесовские модели использовались для взлома кодов немецких подводных лодок.
• Американский математик французского происхождения Бернар Купман помог союзникам определить местонахождение немецких подводных лодок с помощью байесовских моделей для перехвата радиопередач.

Если вы хотите узнать больше о байесовской статистике, ознакомьтесь с расширенной сертификацией upGrad по машинному обучению и облаку , чтобы понять основные концепции с помощью реальных отраслевых проектов и тематических исследований. 12-месячный курс предлагается IIT Madras и поддерживает самостоятельное обучение.

Свяжитесь с нами для получения дополнительной информации.