Régression polynomiale : importance, mise en œuvre étape par étape

introduction

Dans ce vaste domaine du Machine Learning, quel serait le premier algorithme que la plupart d'entre nous aurait étudié ? Oui, c'est la régression linéaire. Étant principalement le premier programme et algorithme que l'on aurait appris dans ses premiers jours de programmation d'apprentissage automatique, la régression linéaire a sa propre importance et sa propre puissance avec un type de données linéaire.

Que se passe-t-il si l'ensemble de données que nous rencontrons n'est pas linéairement séparable ? Que se passe-t-il si le modèle de régression linéaire n'est pas en mesure de dériver une sorte de relation entre les variables indépendantes et dépendantes ?

Il existe un autre type de régression connu sous le nom de régression polynomiale. Fidèle à son nom, la régression polynomiale est un algorithme de régression qui modélise la relation entre la variable dépendante (y) et la variable indépendante (x) sous la forme d'un polynôme de nième degré. Dans cet article, nous allons comprendre l'algorithme et les mathématiques derrière la régression polynomiale ainsi que son implémentation en Python.

Qu'est-ce que la régression polynomiale ?

Comme défini précédemment, la régression polynomiale est un cas particulier de régression linéaire dans lequel une équation polynomiale avec un degré (n) spécifié est ajustée sur les données non linéaires qui forment une relation curviligne entre les variables dépendantes et indépendantes.

y= b 0 + b 1 x 1 + b 2 x 1 2 + b 3 x 1 3 +…… b n x 1 n

Ici,

y est la variable dépendante (variable de sortie)

x1 est la variable indépendante (prédicteurs)

b 0 est le biais

b 1 , b 2 , ….b n sont les poids dans l'équation de régression.

Au fur et à mesure que le degré de l'équation polynomiale ( n ) devient plus élevé, l'équation polynomiale devient plus compliquée et il existe une possibilité que le modèle ait tendance à sur-ajuster ce qui sera discuté dans la partie ultérieure.

Comparaison des équations de régression

Régression linéaire simple ===> y= b0+b1x

Régression Linéaire Multiple ===> y= b0+b1x1+ b2x2+ b3x3+…… bnxn

Régression polynomiale ===> y= b0+b1x1+ b2x12+ b3x13+…… bnx1n

À partir des trois équations ci-dessus, nous voyons qu'il existe plusieurs différences subtiles entre elles. Les régressions linéaires simples et multiples sont différentes de l'équation de régression polynomiale en ce sens qu'elles ont un degré de seulement 1. La régression linéaire multiple se compose de plusieurs variables x1, x2, etc. Bien que l'équation de régression polynomiale n'ait qu'une seule variable x1, elle a un degré n qui la différencie des deux autres.

Besoin de régression polynomiale

À partir des diagrammes ci-dessous, nous pouvons voir que dans le premier diagramme, une ligne linéaire est tentée d'être ajustée sur l'ensemble donné de points de données non linéaires. On comprend qu'il devient très difficile pour une droite d'établir une relation avec ces données non linéaires. Pour cette raison, lorsque nous formons le modèle, la fonction de perte augmente, provoquant une erreur élevée.

D'autre part, lorsque nous appliquons la régression polynomiale, il est clairement visible que la ligne s'adapte bien aux points de données. Cela signifie que l'équation polynomiale qui correspond aux points de données dérive une sorte de relation entre les variables de l'ensemble de données. Ainsi, pour de tels cas où les points de données sont disposés de manière non linéaire, nous avons besoin du modèle de régression polynomiale.

Implémentation de la régression polynomiale en Python

À partir de là, nous allons construire un modèle d'apprentissage automatique en Python implémentant la régression polynomiale. Nous comparerons les résultats obtenus avec la régression linéaire et la régression polynomiale. Comprenons d'abord le problème que nous allons résoudre avec la régression polynomiale.

Description du problème

En cela, considérons le cas d'une Start-up cherchant à embaucher plusieurs candidats d'une entreprise. Il existe différentes ouvertures pour différents postes dans l'entreprise. La start-up a des détails sur le salaire pour chaque rôle dans l'entreprise précédente. Ainsi, lorsqu'un candidat mentionne son salaire précédent, le RH de la start-up doit le vérifier avec les données existantes. Ainsi, nous avons deux variables indépendantes qui sont Position et Niveau. La variable dépendante (sortie) est le salaire qui doit être prédit à l'aide de la régression polynomiale.

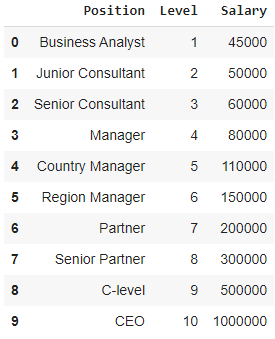
En visualisant le tableau ci-dessus dans un graphique, nous voyons que les données sont de nature non linéaire. En d'autres termes, à mesure que le niveau augmente, le salaire augmente à un rythme plus élevé, ce qui nous donne une courbe comme indiqué ci-dessous.

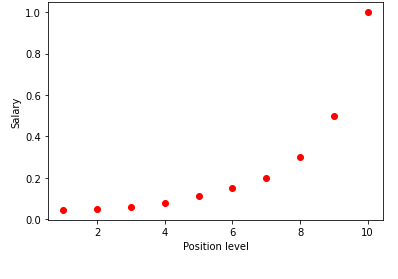
Étape 1 : Prétraitement des donnéesLa première étape de la création d'un modèle d'apprentissage automatique consiste à importer les bibliothèques. Ici, nous n'avons que trois bibliothèques de base à importer. Après cela, l'ensemble de données est importé de mon référentiel GitHub et les variables dépendantes et les variables indépendantes sont affectées. Les variables indépendantes sont stockées dans la variable X et la variable dépendante est stockée dans la variable y.

importer numpy en tant que np

importer matplotlib.pyplot en tant que plt

importer des pandas en tant que pd

jeu de données = pd.read_csv('https://raw.githubusercontent.com/mk-gurucharan/Regression/master/PositionSalaries_Data.csv')

X = dataset.iloc[:, 1:-1].values

y = dataset.iloc[:, -1].values

Ici, dans le terme [:, 1:-1], le premier deux-points représente que toutes les lignes doivent être prises et le terme 1:-1 indique que les colonnes à inclure vont de la première colonne à l'avant-dernière colonne qui est donnée par -1.

Étape 2 : Modèle de régression linéaireDans l'étape suivante, nous allons construire un modèle de régression linéaire multiple et l'utiliser pour prédire les données salariales à partir des variables indépendantes. Pour cela, la classe LinearRegression est importée de la bibliothèque sklearn. Il est ensuite ajusté sur les variables X et y à des fins d'apprentissage.

de sklearn.linear_model importer LinearRegression

régresseur = LinearRegression()

regressor.fit(X, y)

Une fois le modèle construit, en visualisant les résultats, on obtient le graphique suivant.

Comme on le voit clairement, en essayant d'ajuster une ligne droite sur un ensemble de données non linéaires, aucune relation n'est dérivée par le modèle d'apprentissage automatique. Ainsi, nous devons opter pour la régression polynomiale pour obtenir une relation entre les variables.

Étape 3 : Modèle de régression polynomialeDans cette prochaine étape, nous allons ajuster un modèle de régression polynomiale sur cet ensemble de données et visualiser les résultats. Pour cela, nous importons une autre classe du module sklearn nommée PolynomialFeatures dans laquelle nous donnons le degré de l'équation polynomiale à construire. Ensuite, la classe LinearRegression est utilisée pour ajuster l'équation polynomiale au jeu de données.

de sklearn.preprocessing importer PolynomialFeatures

de sklearn.linear_model importer LinearRegression

poly_reg = PolynomialFeatures(degré = 2)

X_poly = poly_reg.fit_transform(X)

lin_reg = RégressionLinéaire()

lin_reg.fit(X_poly, y)

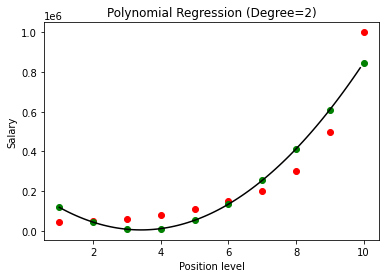
Dans le cas ci-dessus, nous avons donné le degré de l'équation polynomiale comme étant égal à 2. En traçant le graphique, nous voyons qu'il y a une sorte de courbe qui est dérivée mais il y a toujours beaucoup d'écart par rapport aux données réelles (en rouge ) et les points de courbe prédits (en vert). Ainsi, à l'étape suivante, nous augmenterons le degré du polynôme à des nombres plus élevés tels que 3 et 4, puis le comparerons.

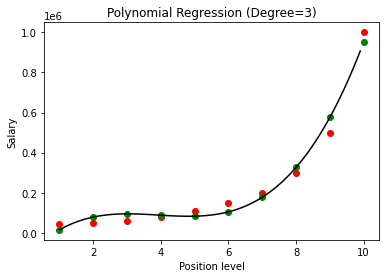
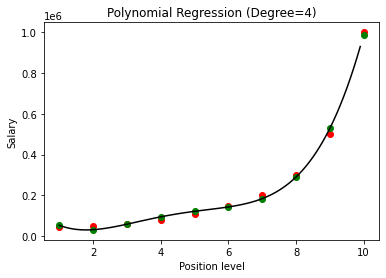
En comparant les résultats de la régression polynomiale avec les degrés 3 et 4, nous voyons qu'à mesure que le degré augmente, le modèle s'entraîne bien avec les données. Ainsi, nous pouvons en déduire qu'un degré plus élevé permet à l'équation polynomiale de s'adapter plus précisément aux données d'apprentissage. Cependant, c'est le cas parfait du surajustement. Ainsi, il devient important de choisir précisément la valeur de n pour éviter le surajustement.

Qu'est-ce que le surajustement ?

Comme son nom l'indique, le surajustement est qualifié de situation dans les statistiques lorsqu'une fonction (ou un modèle d'apprentissage automatique dans ce cas) est trop étroitement ajustée à un ensemble de points de données limités. Cela entraîne une mauvaise performance de la fonction avec de nouveaux points de données.

Dans Machine Learning, si un modèle est surajusté sur un ensemble donné de points de données d'apprentissage, alors lorsque le même modèle est introduit dans un ensemble de points complètement nouveau (disons l'ensemble de données de test), alors il fonctionne très mal sur celui-ci comme le Le modèle de sur-ajustement ne s'est pas bien généralisé avec les données et ne sur-adapte que sur les points de données d'entraînement.

Dans la régression polynomiale, il y a de fortes chances que le modèle soit surajusté aux données d'apprentissage à mesure que le degré du polynôme augmente. Dans l'exemple ci-dessus, nous voyons un cas typique de surajustement dans la régression polynomiale qui peut être corrigé avec seulement une base d'essais et d'erreurs pour choisir la valeur optimale du degré.

Lisez aussi : Idées de projets d'apprentissage automatique

Conclusion

Pour conclure, la régression polynomiale est utilisée dans de nombreuses situations où il existe une relation non linéaire entre les variables dépendantes et indépendantes. Bien que cet algorithme souffre d'une sensibilité aux valeurs aberrantes, il peut être corrigé en les traitant avant d'ajuster la droite de régression. Ainsi, dans cet article, nous avons été initiés au concept de régression polynomiale avec un exemple de son implémentation en programmation Python sur un jeu de données simple.

Si vous souhaitez en savoir plus sur l'apprentissage automatique, consultez le diplôme PG en apprentissage automatique et IA de IIIT-B & upGrad, conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, IIIT- Statut B Alumni, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.

Apprenez le cours ML des meilleures universités du monde. Gagnez des programmes de maîtrise, Executive PGP ou Advanced Certificate pour accélérer votre carrière.

Qu'entendez-vous par régression linéaire ?

La régression linéaire est un type d'analyse numérique prédictive à travers laquelle nous pouvons trouver la valeur d'une variable inconnue à l'aide d'une variable dépendante. Il explique également le lien entre une variable dépendante et une ou plusieurs variables indépendantes. La régression linéaire est une technique statistique permettant de démontrer un lien entre deux variables. La régression linéaire trace une ligne de tendance à partir d'un ensemble de points de données. La régression linéaire peut être utilisée pour générer un modèle de prédiction à partir de données apparemment aléatoires, telles que des diagnostics de cancer ou des cours boursiers. Il existe plusieurs méthodes pour calculer la régression linéaire. L'approche des moindres carrés ordinaires, qui estime les variables inconnues dans les données et se transforme visuellement en la somme des distances verticales entre les points de données et la ligne de tendance, est l'une des plus répandues.

Quels sont certains des inconvénients de la régression linéaire ?

Dans la plupart des cas, l'analyse de régression est utilisée dans la recherche pour établir qu'il existe un lien entre les variables. Cependant, la corrélation n'implique pas la causalité puisqu'un lien entre deux variables n'implique pas que l'une provoque l'autre. Même une ligne dans une régression linéaire de base qui convient bien aux points de données peut ne pas garantir une relation entre les circonstances et les résultats logiques. À l'aide d'un modèle de régression linéaire, vous pouvez déterminer s'il existe ou non une corrélation entre les variables. Une enquête supplémentaire et une analyse statistique seront nécessaires pour déterminer la nature exacte du lien et si une variable cause l'autre.

Quelles sont les hypothèses de base de la régression linéaire ?

Dans la régression linéaire, il y a trois hypothèses clés. Les variables dépendantes et indépendantes doivent, avant tout, avoir une connexion linéaire. Un diagramme de dispersion des variables dépendantes et indépendantes est utilisé pour vérifier cette relation. Deuxièmement, il devrait y avoir une multicolinéarité minimale ou nulle entre les variables indépendantes de l'ensemble de données. Cela implique que les variables indépendantes ne sont pas liées. La valeur doit être limitée, ce qui est déterminé par l'exigence du domaine. L'homoscédasticité est le troisième facteur. L'hypothèse selon laquelle les erreurs sont uniformément réparties est l'une des hypothèses les plus essentielles.