Implementar el algoritmo de clasificación de conteo en Java

Publicado: 2023-01-30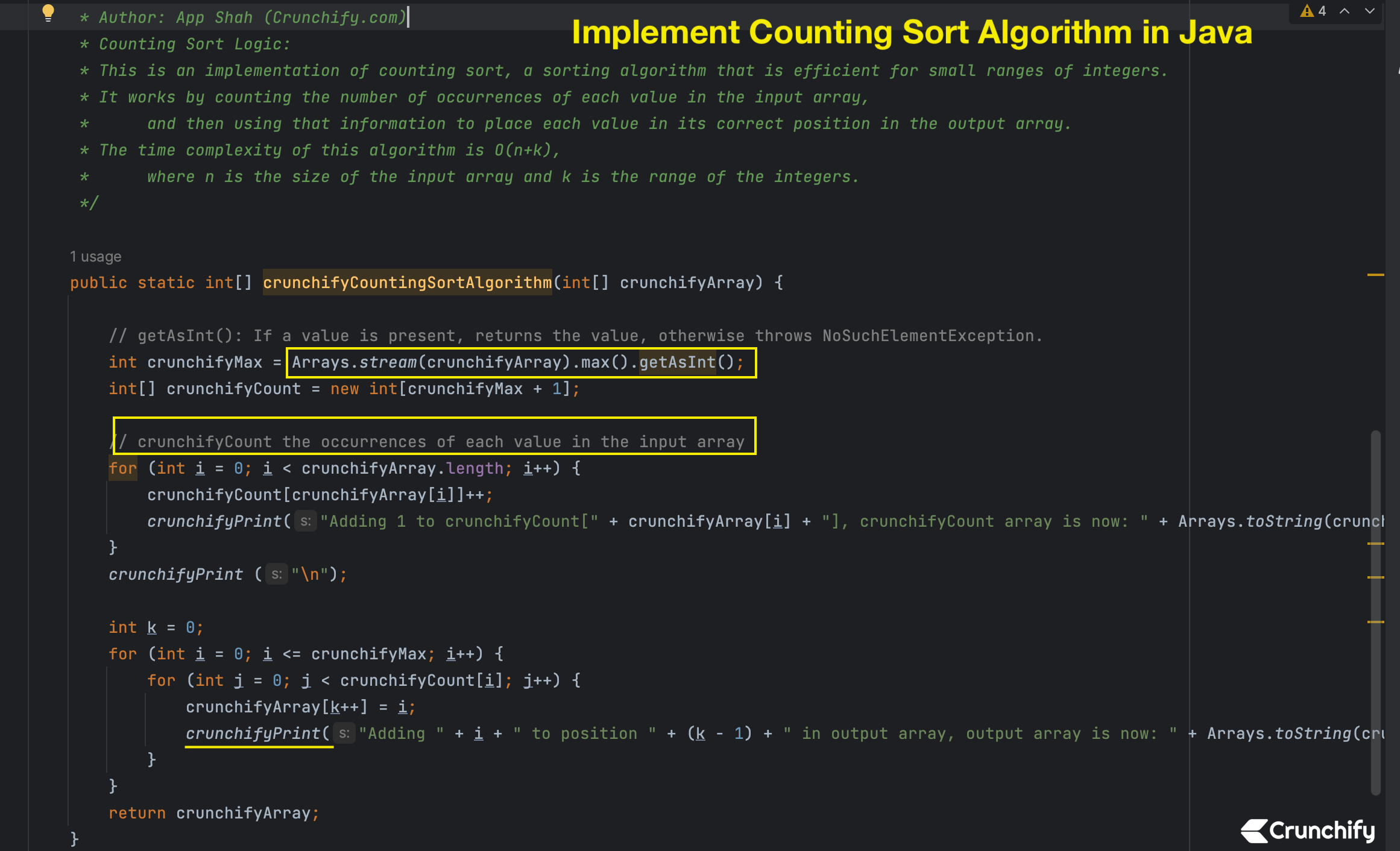
Implementar el algoritmo de clasificación de conteo en Java

¿Qué es el algoritmo de clasificación de conteo?

Clasificación por conteo, un algoritmo de clasificación que es eficiente para small ranges of integers . Funciona contando el número de ocurrencias de cada valor en la matriz de entrada y luego usando esa información para colocar cada valor en su posición correcta en la matriz de salida.

La complejidad temporal de este algoritmo es O(n+k) , donde n es el tamaño de la matriz de entrada y k es el rango de los números enteros.

CrunchifyCountingSortAlgo.java

Aquí hay una implementación completa de Counting Sort en Java. Simplemente cópielo en su IDEA preferida y ejecútelo.

 paquete crunchify.com.java.tutorials;

importar java.util.Arrays;

/**
 * @autor Crunchify.com
 * Programa: ¿Cómo implementar el algoritmo de clasificación de conteo en Java?
 * Counting sort es un algoritmo de clasificación que ordena los elementos de una matriz 
 * contando el número de ocurrencias de cada elemento único en la matriz.
 */

clase pública CrunchifyCountingSortAlgo {

    public static void main(String[] args) {

        // Matriz entera de 10 elementos
        int[] crunchifyArray = {9, 3, 6, 6, 1, 12, 32, 29, 2, 9, 3};

        crunchifyPrint("Array original: " + Arrays.toString(crunchifyArray));
        crunchifyPrint ("\n");

        CrunchifyCountingSortAlgo crunchify = new CrunchifyCountingSortAlgo();
        crunchify.crunchifyCountingSortAlgorithm(crunchifyArray);

        crunchifyPrint ("\n");
        crunchifyPrint("Resultado del algoritmo de clasificación de conteo de Crunchify: " + Arrays.toString(crunchifyArray));
    }

    vacío estático privado crunchifyPrint(String s) {

        System.out.println(s);
    }


    /**
     * Autor: Aplicación Shah (Crunchify.com)
     *
     * Lógica de clasificación de conteo:
     * Esta es una implementación de clasificación por conteo, un algoritmo de clasificación que es eficiente para pequeños rangos de números enteros.
     * Funciona contando el número de ocurrencias de cada valor en la matriz de entrada,
     * y luego usar esa información para colocar cada valor en su posición correcta en la matriz de salida.
     * La complejidad temporal de este algoritmo es O(n+k),
     * donde n es el tamaño de la matriz de entrada y k es el rango de los enteros.
     */


    public static int[] crunchifyCountingSortAlgorithm(int[] crunchifyArray) {

        // getAsInt(): si hay un valor presente, devuelve el valor; de lo contrario, lanza NoSuchElementException.
        int crunchifyMax = Arrays.stream(crunchifyArray).max().getAsInt();
        int[] crunchifyCount = new int[crunchifyMax + 1];

        // crunchifyCuenta las ocurrencias de cada valor en la matriz de entrada
        for (int i = 0; i < crunchifyArray.length; i++) {
            crunchifyCount[crunchifyArray[i]]++;
            crunchifyPrint("Agregando 1 a crunchifyCount[" + crunchifyArray[i] 
                    + "], la matriz crunchifyCount ahora es: " + Arrays.toString(crunchifyCount));
        }

        crunchifyPrint ("\n");

        int k = 0;
        para (int i = 0; i <= crunchifyMax; i++) {
            for (int j = 0; j < crunchifyCount[i]; j++) {
                crunchifyArray[k++] = i;
                crunchifyPrint("Agregando " + i + " a la posición " + (k - 1) 
                        + " en la matriz de salida, la matriz de salida ahora es: " + Arrays.toString(crunchifyArray));
            }
        }

        volver crunchifyArray;
    }

}

Simplemente ejecute el programa anterior como una aplicación Java en IntelliJ IDEA o Eclipse IDE y obtendrá el siguiente resultado.

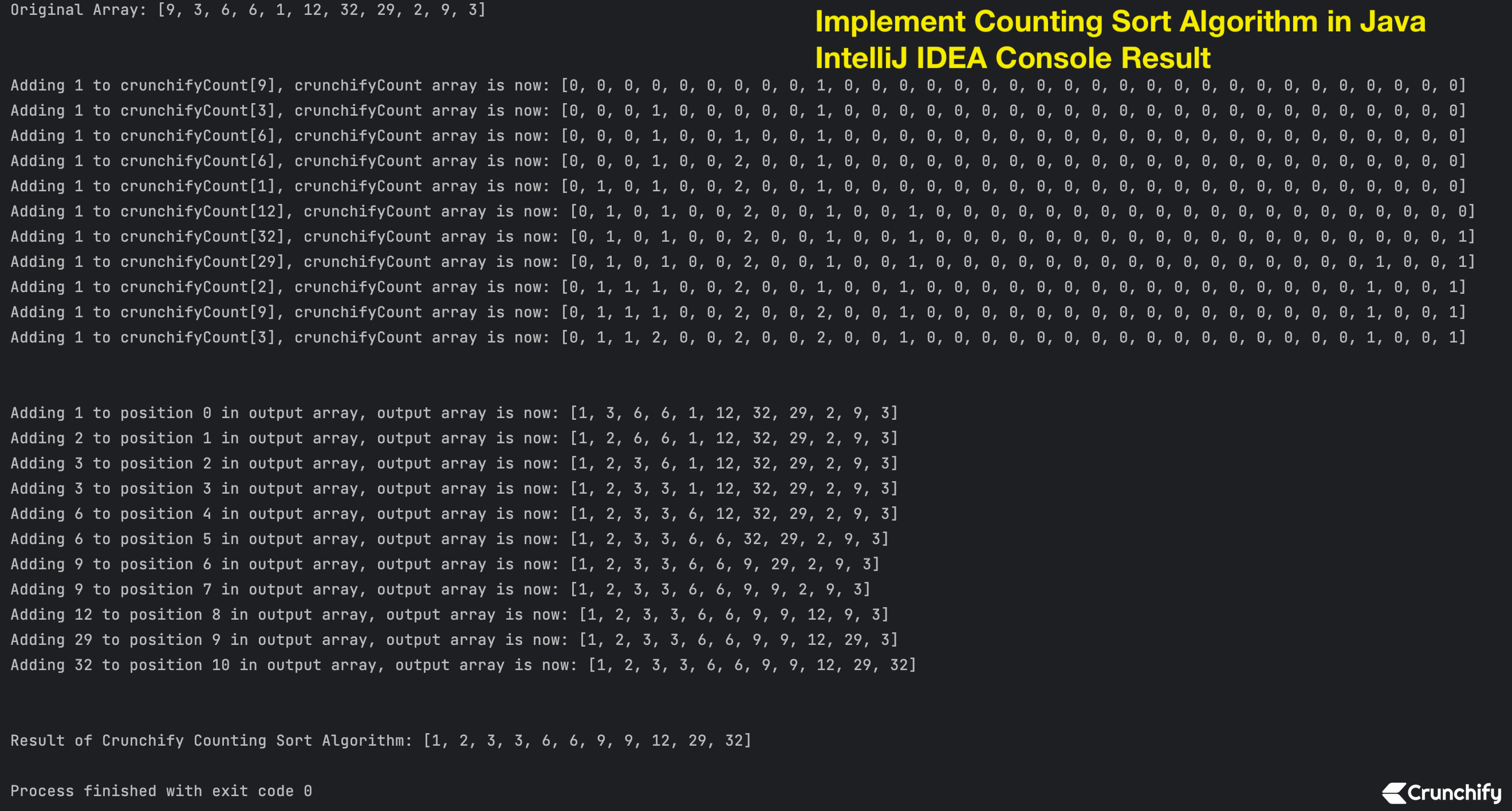
Resultado de la consola IntelliJ IDEA

 Matriz original: [9, 3, 6, 6, 1, 12, 32, 29, 2, 9, 3]


Agregando 1 a crunchifyCount[9], la matriz crunchifyCount ahora es: [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Agregando 1 a crunchifyCount[3], la matriz crunchifyCount ahora es: [0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Agregando 1 a crunchifyCount[6], la matriz crunchifyCount ahora es: [0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Agregando 1 a crunchifyCount[6], la matriz crunchifyCount ahora es: [0, 0, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Agregando 1 a crunchifyCount[1], la matriz crunchifyCount ahora es: [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Agregando 1 a crunchifyCount[12], la matriz crunchifyCount ahora es: [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Agregando 1 a crunchifyCount[32], la matriz crunchifyCount ahora es: [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
Agregando 1 a crunchifyCount[29], la matriz crunchifyCount ahora es: [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1]
Agregando 1 a crunchifyCount[2], la matriz crunchifyCount ahora es: [0, 1, 1, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1]
Agregando 1 a crunchifyCount[9], la matriz crunchifyCount ahora es: [0, 1, 1, 1, 0, 0, 2, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1]
Agregando 1 a crunchifyCount[3], la matriz crunchifyCount ahora es: [0, 1, 1, 2, 0, 0, 2, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1]


Agregando 1 a la posición 0 en la matriz de salida, la matriz de salida ahora es: [1, 3, 6, 6, 1, 12, 32, 29, 2, 9, 3]
Agregando 2 a la posición 1 en la matriz de salida, la matriz de salida ahora es: [1, 2, 6, 6, 1, 12, 32, 29, 2, 9, 3]
Agregando 3 a la posición 2 en la matriz de salida, la matriz de salida ahora es: [1, 2, 3, 6, 1, 12, 32, 29, 2, 9, 3]
Agregando 3 a la posición 3 en la matriz de salida, la matriz de salida ahora es: [1, 2, 3, 3, 1, 12, 32, 29, 2, 9, 3]
Agregando 6 a la posición 4 en la matriz de salida, la matriz de salida ahora es: [1, 2, 3, 3, 6, 12, 32, 29, 2, 9, 3]
Al agregar 6 a la posición 5 en la matriz de salida, la matriz de salida ahora es: [1, 2, 3, 3, 6, 6, 32, 29, 2, 9, 3]
Agregando 9 a la posición 6 en la matriz de salida, la matriz de salida ahora es: [1, 2, 3, 3, 6, 6, 9, 29, 2, 9, 3]
Al agregar 9 a la posición 7 en la matriz de salida, la matriz de salida ahora es: [1, 2, 3, 3, 6, 6, 9, 9, 2, 9, 3]
Agregando 12 a la posición 8 en la matriz de salida, la matriz de salida ahora es: [1, 2, 3, 3, 6, 6, 9, 9, 12, 9, 3]
Al agregar 29 a la posición 9 en la matriz de salida, la matriz de salida ahora es: [1, 2, 3, 3, 6, 6, 9, 9, 12, 29, 3]
Agregando 32 a la posición 10 en la matriz de salida, la matriz de salida ahora es: [1, 2, 3, 3, 6, 6, 9, 9, 12, 29, 32]


Resultado del algoritmo de clasificación de conteo de Crunchify: [1, 2, 3, 3, 6, 6, 9, 9, 12, 29, 32]

Proceso finalizado con código de salida 0
Implementar el algoritmo de clasificación de conteo en Java - Resultado de IntelliJ IDEA

Avíseme si tiene algún problema al ejecutar el programa Java Counting Sort Algorithm.